電界強度と受信電力

はじめに

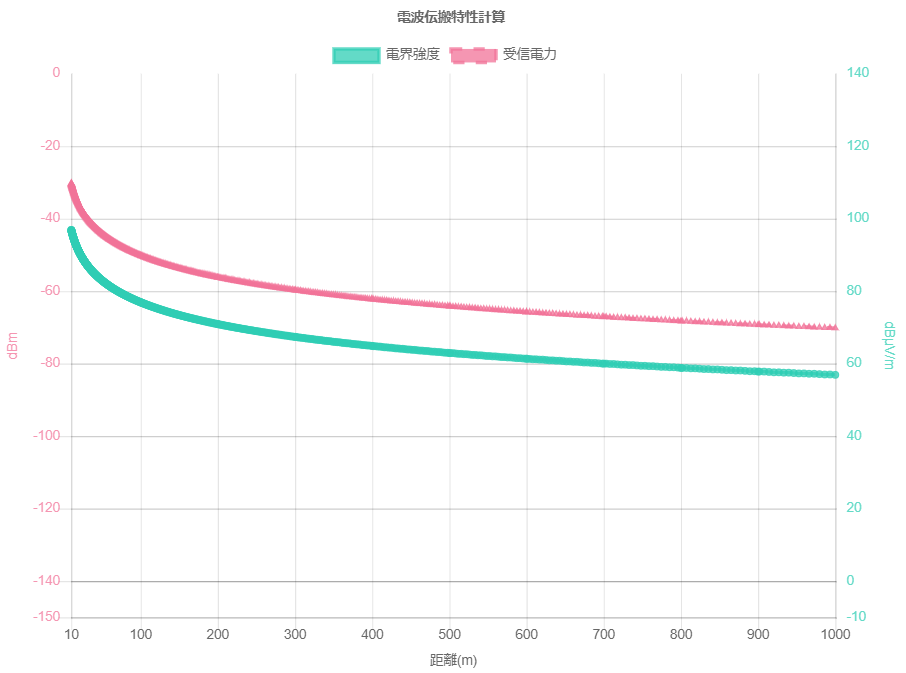
当社の電波伝搬特性の計算ツールでシミュレーションを行うと結果として電界強度と受信電力の2つの結果を得ることができます。いずれも距離とともに電界強度・受信電力が減衰しますが、その違いについて記載したいと思います。

電波の放射

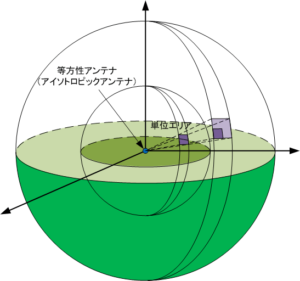電波の放射については「電波とは」の「電波の放射」で少し触れましたが、図にあるようにアンテナから立体的に放射状に広がっていきます。エネルギーは面で考えるとわかりやすく、距離が2倍になると面は2×2で4倍になりますのでエネルギーの密度で考えると1/4になります。つまり単位面あたりのエネルギーは距離の2乗で減衰します。

電界強度

電界強度は、上記の放射状に広がったエネルギーを1[m]あたりの電圧で示したもので単位は[V/m]を用います（デシベル単位の[dBV/m]を用いる場合もあります）。電界強度Eは以下のような数式で求めることができます。

$$E (^V/_m)=\frac{\sqrt{30GtPt}}{d}$$

$$E (^{dBV}/_m)=20\log\biggl(\frac{\sqrt{30PtGt}}{d}\biggr)$$

Pt: 実効放射電力 [W]、d: 送受信点間距離 [m]、Gt: 送信アンテナの絶対利得 [真数]

距離dが2倍になれば電界強度Eは1/2になります（デシベルの場合6 [dB]小さくなります）。距離に反比例して減衰します。

意外に思われる方もいると思いますが、電界強度Eは1[m]あたりの電圧のため、波長λ（周波数）に依存せず実効放射電力と送受信点間距離で決まります。つまり電界強度は周波数が異なっても同じになります。

受信電力

一方受信電力は実際にアンテナで受信する電力になります。受信電力は距離以外に送受信のアンテナのゲインや周波数に依存します。

送受信点間距離d [m]での電波の伝搬損失量[dB]は、

$$Loss(dB)=20\log(\frac{4πd}{λ})$$

となります。ちなみに波長λ [m]は周波数に反比例します。

$$λ=\frac{c(^m/_s)}{f(MHz)}=\frac{3\times10^8}{f\times10^6}$$

上記より受信電力Pr [dBm]は、

$$Pr = Pt + Gt + Gr – 20\log(\frac{4πd}{λ})$$

Pr: 送信電力 [dBm]、Gt: 送信アンテナの利得 [dBi]、Gr: 受信アンテナ利得 [dBi]

となります。わかりやすいように送受信のアンテナは0[dBi]アイソトロピックアンテナで考えると、

$$Gr = Pt – 20\log(\frac{4πd}{λ})$$

となります。

受信電力は距離dが2倍になれば6[dB]小さくなります（1/4倍）。また周波数fが2倍になれば[6dB]小さくなります（1/4倍）。距離・周波数に対してそれぞれ2乗で減衰します。

電界強度とは異なり、距離が同じでも周波数が高くなると受信電力は減少します。

距離と周波数への依存

電界強度と受信電力については、距離が離れるとともにどちらも減衰しますが、周波数に対しては受信電力が高くなるにつれて減衰するのに対し、電界強度は変わりません。

電界強度は単位の[V/m]または[dBuV/m]からわかるように[m]あたりの電界強度のため周波数に対する依存がありませんが、受信電力の場合は例えばダイポールアンテナを例にするとアンテナの長さは波長λに依存するため、同じ2.14[dBi]のアンテナでも周波数が高くなるとアンテナの長さは短くなり受信電力は小さくなります。

参考までに電界強度E₀によって生じる半波長ダイポールアンテナの起電力V₀ [m]は以下のような式で表すことができます。

$$V_0 = E_0l_{eff}$$

l_effは受信アンテナの実効長[m]ですので $$l_{eff} = \frac{λ}{π}$$ で示すことができ、

$$V_0 (V) = \frac{E_0λ}{π}$$

になりますので、起電力が波長λに依存していることがわかります。

ではアンテナを長くすればよいのか

受信電力を上げるために単純にアンテナを長くすればということになりますが、「アンテナ」の説明で記載したように波長に合わせてアンテナをマッチングしないと上手く電波を送受信することができません。また電波を送信する場合はアンテナゲインが高すぎると電波法違反になるため単純にアンテナを大きくするわけにはいきません。

またあくまでも計算上の結果のため、実際には偏波面、位相、障害物の有無などによる影響も考慮する必要があります。